Plošné zatížení, tlak

Plošné zatížení působící na stěnu prvku lze předepsat v libovolném zatěžovacím stavu. Speciálním případem obecného plošného zatížení je tlak, který se s výhodou zadá v lokálním systému vnější normály.

V souboru name.i2 se nejprve definuje vektor pomocí sady:

SV číslo sady T 9 V $q_x$ $q_y$ $q_z$

nebo

SV číslo sady T 6 V $q_n$

a takto definovaná sada se následně přiřadí stěně vybraných prvků:

AS číslo zatěžovacího stavu /$\dots$ /S číslo sady E seznam čísel prvků S číslo stěny /$\dots$

přičemž

$q_x,q_y,q_z~[\text{Pa}]$ jsou složky napětí ve směru globálních os,
$q_n~[\text{Pa}]$ je napětí kolmé na stěnu prvku a působící ve směru vnější normály stěny prvku (tlak $p$ se zadává záporně, tj. $q_n=-p$).

Poznámka
Stěny a jejich lokální čísla jsou definovány pro isoparametrické prvky a prvky semi-loof, viz Referenční příručka. U 2D isoparametrických prvků se za stěnu prvku považuje jeho hrana, protože má nenulovou tloušťku (a tedy i plochu). U prvků semi-loof je definována jen jedna stěna (střednicová plocha), jejíž orientace je dána normálou $\zeta,$ viz Referenční příručka. Záporně zadaný tlak působí na horní stranu plochy, kladně zadaný tlak působí na spodní stranu plochy.

Poznámka
V jednom zatěžovací stavu se může vyskytovat více přiřazení plošných sil jedné stěně prvku. V takovém případě se složky sil sčítají.

Poznámka
Složky vektoru mohou záviset na globálních souřadnicích $x,y,z$ s využitím všech funkčních závislostí, viz Referenční příručka.

Příklad

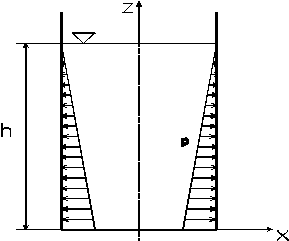
Uvažujme hydrostatický tlak vody $p=rg(h-z)$ působící na stěnu nádoby $h=5~\text{m},$ takže $rg=10000~\text{Pa/m}$ a $rgh=50000~\text{Pa}.$

Závislost tlaku $p$ na souřadnici $z$ popíšeme pomocí polynomiální závislosti $p(z)=50000-10000z,$ viz Referenční příručka. Globální souřadnice $z$ má podle Referenční příručky identifikační číslo 3, odtud

SV 1 T -6 I 3 V -50000 10000

Při zadání tlaku $-p$ sadou 1 jsme mlčky předpokládali, že normály všech skořepinových prvků směřují dovnitř nádoby. Smysl normál je však určen topologií prvků a normály všech prvků nemusí být shodně orientovány, viz Referenční příručka. Proto definujeme další sadu

SV 2 T -6 I 3 V 50000 -10000

kterou přiřadíme prvkům, jejichž normála směřuje ven z nádoby.

Přiřazení bude mít tvar

AS <stav> / …
  /S 1 E <prvky> S 1 ; prvky s normálou směřující dovnitř
  /S 2 E <prvky> S 1 ; prvky s normálou směřující ven
  / …