Liniové zatížení

Liniové zatížení působící na hranu prvku lze předepsat v libovolném zatěžovacím stavu.

V souboru name.i2 se nejprve definuje vektor pomocí sady:

LV číslo sady T 9 V $l_x$ $l_y$ $l_z$

nebo

LV číslo sady T 6 V $l_{x_h}$ $l_{y_h}$ $l_{z_h}$ $m_{y_h}$

a takto definovaná sada se následně přiřadí hraně vybraných prvků:

AS číslo zatěžovacího stavu /$\dots$ /L číslo sady E seznam čísel prvků L číslo hrany /$\dots$

přičemž

$l_x,l_y,l_z~[\text{N/m}]$ jsou složky síly ve směru globálních os,
$l_{x_h},l_{y_h},l_{z_h}~[\text{N/m}]$ jsou složky síly na hranu prvku semi-loof ve směru lokálních os, viz Referenční příručka,
$m_{y_h}~[\text{Nm/m}]$ je moment na hranu prvku semi-loof, viz Referenční příručka.

Poznámka
Hrany a jejich lokální čísla jsou definovány pro 3D isoparametrické prvky a prvky semi-loof, viz Referenční příručka. U nosníkových prvků se spojité zatížení zadává formou objemových sil $Q=\text{liniová síla}/\text{průřez}~[\text{N/m}^3].$ Obdobně u 2D isoparametrických prvků se spojité zatížení zadává formou plošných sil $q=\text{liniová síla}/\text{tloušťka}~[\text{N/m}^2].$

Poznámka
V jednom zatěžovací stavu se může vyskytovat více přiřazení liniových sil jedné hraně prvku. V takovém případě se složky sil sčítají.

Poznámka
Složky vektoru mohou záviset na globálních souřadnicích $x,y,z$ s využitím všech funkčních závislostí, viz Referenční příručka.

Příklad

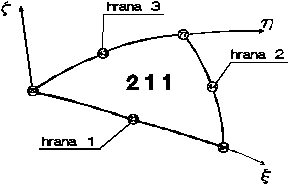
Uvažujme trojúhelníkový skořepinový prvek. Globální čísla uzlů vyplývají z konkretního očíslování sítě.

Podle Referenční příručky je topologie prvku definována posloupností čísel uzlů

22 24 77 23 44 43

a orientace hrany 2 je následující:

osa $x_h$ směřuje ven z prvku,
osa $y_h$ je orientována od uzlu 24 směrem k uzlu 77,
osa $z_h$ směřuje nahoru (pravotočivě 22–24–77).

Pokud je síla zadána v globálním systému $x,y,z$ jako $[l_x,l_y,l_z],$ není znalost orientace hrany potřebná.

Přiřazení může mít například tvar

AS <stav> /… /L <sada> E 211 L 2/ …