Nenulové složky posunutí a natočení uzlu
Lineární úlohy
Nenulové složky posunutí a natočení v uzlu (nehomogenní okrajová podmínka) se předepisují povinně v prvním zatěžovacím stavu a platí pro všechny zatěžovací stavy.
V souboru name.i2 se nejprve definuje vektor pomocí sady:
NV číslo sady T 1 V $u$ $v$ ; 2 složky NV číslo sady T 1 V $u$ $v$ $w$ ; 3 složky NV číslo sady T 1 V $u$ $v$ $w$ $\alpha$ $\beta$ ; 5 složek NV číslo sady T 1 V $u$ $v$ $w$ $\varphi_x$ $\varphi_y$ $\varphi_z$ ; 6 složek
podle počtu složek v uzlu, nebo
NV číslo sady T 1 C seznam čísel složek V předepsané hodnoty
a takto definovaná sada se následně přiřadí vybraným uzlům:
AS 1 /$\dots$ /N číslo sady N seznam čísel uzlů /$\dots$
První typ sady se použije pro předpis všech stupňů volnosti v uzlu. Vektor může být přiřazen jen těm uzlům, které mají stejný nebo větší počet stupňů volnosti, než je počet předepsaných hodnot. Případné chybějící hodnoty jsou považovány za nulové.
Druhý typ sady se použije tehdy, je-li třeba předepsat hodnoty jen některých stupňů volnosti v uzlu a ostatní mají zůstat volné. Vektor může být přiřazen jen těm uzlům, které mají všechny složky zapsané za klíčovým písmenem C.
Čísla složek (stupňů volnosti) vyplývají z tabulky:
| Číslo | Složka | Význam |
|---|---|---|
| 1 | $u$ | posunutí ve směru osy $x$ $\text{[m]}$ |
| 2 | $v$ | posunutí ve směru osy $y$ $\text{[m]}$ |
| 3 | $w$ | posunutí ve směru osy $z$ $\text{[m]}$ |
| 4 | $\alpha$ | úhel natočení hrany prvku semi-loof $\text{[rad]},$ viz Referenční příručka |
| 4 | $\varphi_x$ | úhel natočení okolo osy $x$ $\text{[rad]},$ viz Referenční příručka |
| 5 | $\beta$ | úhel natočení hrany prvku semi-loof $\text{[rad]},$ viz Referenční příručka |
| 5 | $\varphi_y$ | úhel natočení okolo osy $y$ $\text{[rad]},$ viz Referenční příručka |
| 6 | $\varphi_z$ | úhel natočení okolo osy $z$ $\text{[rad]},$ viz Referenční příručka |
Příklad
Uvažujme dvě NV sady s rozlišovacími čísly 1 a 2:
NV 1 T 1 V 0 0.001 0 NV 2 T 1 C 6 V 1e-3
První sada popisuje posunutí $1~\text{mm}$ ve směru osy $y$ (ostatní DOF jsou fixovány).
Druhá sada předepisuje úhel natočení $\varphi_z=10^{-3}~\text{rad}$ (ostatní DOF jsou volné).
Sadu NV 1 lze přiřadit kterémukoliv uzlu, sadu NV 2 jen uzlu nosníkového prvku.
Přiřazení může mít například tvar
… /N 1 N 23 24 109/N 2 N 35/ …
kdy vektor posunutí uzlů 23, 24 a 109 bude pevně dán jako $[0;0{,}001;0],$ nebo $[0;0{,}001;0;0;0],$ nebo $[0;0{,}001;0;0;0;0],$ podle typu uzlu. Uzel 35 musí příslušet nosníkovému prvku a předepsáno v něm bude jen natočení $\varphi_z$; ostatní DOF budou neznámé.
Nelineární úlohy
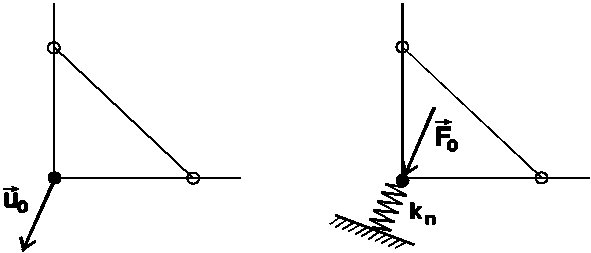
V nelineárních úlohách připouští systém PMD jen jediný způsob, jak vynutit nenulové posunutí (deformační zatížení). Tím je metoda pokutové funkce – penalty. Uvažujme část sítě na obrázku, kdy je uzlu předepsán posuv $\mathbf{u}_0.$
Zvolenému uzlu se nejprve přiřadí pružina o tuhosti $k_n$ ve směru daném vektorem $\mathbf{u}_0.$ Tuhost $k_n$ by měla být přibližně o 6 řádů vyšší, než je lokální tuhost tělesa (což lze alespoň řádově odhadnout). Dále se přiřadí uzlová síla $\mathbf{F}_0=k_n\mathbf{u}_0,$ která vynutí na pružině posuv $\mathbf{u}_0.$ Protože je tuhost pružiny podstatně větší než tuhost tělesa, dá se očekávat, že i skutečný posuv bude blízký $\mathbf{u}_0.$
Všechny potřebné pružiny se definují v dávce AS 1 a adekvátní uzlové síly v dávkách AS 2 a vyšších. Jestliže libovolný zatěžovací stav obsahuje diskretní sílu $\mathbf{F}$ v uzlu s velmi tuhou pružinou, znamená to, že v tomto zatěžovacím stavu bude vynucen posuv $\mathbf{u}=\mathbf{F}/k_n.$ Pokud v některém zatěžovacím stavu chybí předpis takové síly, bude posuv uzlu přibližně nulový.