Table of Contents
Response spectrum, BEAM53D4
Problem
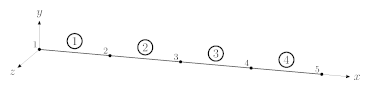
Mesh
Boundary conditions
$u=v=w=\varphi_x=\varphi_y=\varphi_z=0$ at node 1
Computation
The only input for the response spectrum method is the set of spectral accelerations corresponding to the loading and damping given. Let us denote the base acceleration as $$a(t)=\ddot W(t)=-\omega^2 W_0\sin\omega t.$$ A characteristic equation of the linear harmonic oscillator $(\omega_k,\xi_k)$ exited kinematically by $W(t)$ has the form $$\ddot x_k(t)+2\xi_k\omega_k\dot x_k(t)+\omega_k^2x_k(t)=-a(t)$$ with the solution $$x_k(t)=A_ke^{-\xi_k\omega_k t}\sin(\bar\omega_k t+\varphi_k)+x_{pk}(t),$$ where $A_k,$ $\varphi_k$ are constants to be determined from the initial conditions $$x_k(0)=\dot x_k(0)=0$$ and $\bar\omega_k$ is the damped angular frequency $$\bar\omega_k=\omega_k\sqrt{1-\xi_k^2}.$$ Global acceleration can be computed as $$g_k(t)=a(t)+\ddot x_k(t)$$ and its maximum $$G_k=\max_t\vert g_k(t)\vert=G_k(\omega_k,\xi_k)$$ which is also called the spectral acceleration. Thus, it is sufficient for us to calculate $G_k$ as functions of $(\omega_k,\xi_k)$ for the base acceleration $a(t)$ defined above. In this particular example we make use of the steady-state part of the solution only, which yields $$\begin{align} G_k&\simeq\max\limits_t\vert a(t)+x_{pk}(t)\vert\le\max\limits_t\vert x_{pk}(t)\vert \\ &=\omega^2W_0+\omega^4W_0\left[(\omega_k^2-\omega^2)^2 + 4(\xi_k\omega_k\omega)^2\right]^{-\frac{1}{2}}. \end{align}$$ Substituting for $\omega_k=2\pi f_k$ with $f_k$ read from the table shown in Natural frequencies for the beam element we finally obtain
| $k$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| $G_k\text{ [m/s}^2\text{]}$ | $0.8787$ | $0.7045$ | $0.6647$ | $0.6615$ | $0.6610$ | $0.6606$ | $0.6606$ | $0.6605$ | $0.6605$ | $0.6605$ |
Note that the FEM results are related to the reference frame that moves with the basis. For example, the total $z$-displacement must be calculated as $$w_p=W_0+w_\text{FEM}.$$
The computation is executed with the following commands:
- beam53d4.bat
rmd3 beam53d4.i1 rpd3 beam53d4.i2 srh3 beam53d4.i3 fefs beam53d4.i4 hmot beam53d4.iM heig beam53d4.iE hmod beam53d3.iD
Input
- beam53d4.i1
; NELEM NNOD ITED IP 4 5 53 ; CRIT SCALE ... RP 1.01 1 8*0 ; default values of cross-sectional characteristics ; A Ik Wk Ieta 2e-4 6.6666666666e-9 6.666666666666e-7 1.66666666666e-9 ; Weta Izeta Wzeta Px Py Pz 3.33333333333e-7 6.66666666666666e-9 6.666666666666e-7 0 1 0 XY N 1:5 X 5*0:1 Y 5*0 Z 5*0 EL E 1:4 N 1 2 2 3 3 4 4 5 EN EN
- beam53d4.i2
; KREST IP 1 ; E α ν ρ MP 1 T 1 V 2e11 0 0.3 7800 AS 1 /M 1 /B 0 N 1 EN EN
- beam53d4.i3
; KREST IP 1 EN EN
- beam53d4.i4
; KREST IP 1 EN EN
- beam53d4.iM
; KDIAG KPRIN IP 1 0 EN EN
- beam53d4.iE
; KREST NROOT NITERX KTPR KEVP IP 1 10 0 0 0 EN EN
- beam53d4.iD
; KOUT KDUMP KPRIN KKIN IP 3 0 0 2 ; TEND DT RP 0 0 VC 1 T 1 R ; spectrum acceleration ; x-direction 10*0 ; y-direction 10*0 ; z-direction 0.8787 0.7045 0.6647 0.6615 0.6610 2*0.6606 3*0.6605 ; spectrum acceleration AS 3 T 1 I 1 12 EN EN
Output
- beam53d4.oD
; KOUT KDUMP KPRIN KKIN IP 3 0 0 2 ; TEND DT RP 0 0 VC 1 T 1 R ; spectrum acceleration ; x-direction 10*0 ; y-direction 10*0 ; z-direction 0.8787 0.7045 0.6647 0.6615 0.6610 2*0.6606 3*0.6605 ; spectrum acceleration AS 3 T 1 I 1 12 EN EN MODAL PARTICIPATION FACTORS [kg] - 'X' 0.2002E-38 0.5551E-38 0.5239E-38 0.5665E-33 0.9904E-30 0.9592E-23 0.2227E-23 0.8465E-17 0.1207E-16 0.9923E-12 PERCENTAGE OF TOTAL MASS: 0 % out of 0.1560E+01 [kg] MODAL PARTICIPATION FACTORS [kg] - 'Y' 0.2823E-41 0.9564E+00 0.2957E-26 0.2936E+00 0.4488E-30 0.3117E-23 0.1003E+00 0.2976E-17 0.4685E-01 0.3613E-12 PERCENTAGE OF TOTAL MASS: 89 % out of 0.1560E+01 [kg] MODAL PARTICIPATION FACTORS [kg] - 'Z' 0.9564E+00 0.1221E-32 0.2936E+00 0.2141E-37 0.1003E+00 0.4685E-01 0.9472E-26 0.2412E-01 0.2538E-19 0.2188E-14 PERCENTAGE OF TOTAL MASS: 91 % out of 0.1560E+01 [kg] SUM OF REACTIONS 0.1360399253716155E-07 0.7245274126714700E-09 0.8594264947846466E+00 REACTIONS 1 0.13604E-007 0.72453E-009 0.85943E+000 2 0.00000E+000 0.00000E+000 0.00000E+000 3 0.00000E+000 0.00000E+000 0.00000E+000 4 0.00000E+000 0.00000E+000 0.00000E+000 5 0.00000E+000 0.00000E+000 0.00000E+000 AMPLITUDE OF THE STATIONARY SOLUTION TIME T = 0.000000E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.00000E+000 2 0.85025E-016 0.13088E-015 0.50732E-004 3 0.64571E-016 0.46235E-016 0.17691E-003 4 0.35215E-016 0.18208E-015 0.34264E-003 5 0.91148E-016 0.37150E-015 0.52095E-003 VELOCITY 1 0.00000E+000 0.00000E+000 0.00000E+000 2 0.28354E-012 0.43880E-012 0.27252E-002 3 0.21533E-012 0.15661E-012 0.91805E-002 4 0.11744E-012 0.60927E-012 0.17614E-001 5 0.30396E-012 0.12421E-011 0.26837E-001 ACCELERATION 1 0.00000E+000 0.00000E+000 0.00000E+000 2 0.94556E-009 0.14717E-008 0.40866E+000 3 0.71809E-009 0.53094E-009 0.64583E+000 4 0.39163E-009 0.20393E-008 0.94195E+000 5 0.10137E-008 0.41540E-008 0.15573E+001 * END OF HMOD * TOTAL CPU: 00:00:00