Table of Contents
Direct integration, BEAM53D3
Problem
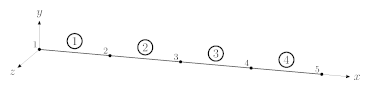
Mesh
Boundary conditions
$u=v=w=\varphi_x=\varphi_y=\varphi_z=0$ at node 1
Computation
In this example, an appropriate time step for the Newmark method can be best derived from the first natural period $T_1$ (see Natural frequencies) as $$\mathtt{TSTEP}=T_1/16=7.640428\times10^{-3}\text{ s}$$ and the end-time must be chosen sufficiently large so that the transient response will diminish. We have shown in Transient response that the amplitude of the transient part would decay exponentially $$\frac{w(\mathbf{x},5T_1)}{w(\mathbf{x},0)}=e^{-10\pi\xi_1}=0.0432,$$ thus, we set $\mathtt{TEND}=5T_1=0.611\text{ s}$ and round it up to an integer multiple of the time step $$\mathtt{TEND}=80\times\mathtt{TSTEP}=0.61123424\text{ s}.$$ The most difficult task is to propose the damping matrix which must be formed explicitly. We can use the Rayleight damping matrix $$\mathbf{C}=\alpha\mathbf{K}+\beta\mathbf{M}$$ or if transformed to the modal basis $$2\omega_k\xi_k=\alpha\omega_k^2+\beta\quad\text{for}\quad k=1,2,\ldots.$$ Obviously, the equations cannot be solved uniquely as we have only two free parameters. We know, however, that the response will presumably consist of bending modes, therefore, we select the first and third equation corresponding to bending in the $x$-$y$ plane $$\begin{align} 2\omega_1\xi_1 &= \alpha\omega_1^2+\beta \\ 2\omega_3\xi_3 &= \alpha\omega_3^2+\beta \end{align}$$ from which $$\alpha=5.3495239\times10^{-4}\text{ s},\quad \beta=8.8663179\text{ s}^{-1}$$ Conversely, the actual values of the modal damping parameters introduced by Rayleigh’s matrix are shown in table below.
| $k$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
|---|---|---|---|---|---|---|---|---|---|---|
| $\xi_k$ | $0.10$ | $0.07$ | $0.10$ | $0.18$ | $0.25$ | $0.48$ | $0.49$ | $0.89$ | $0.96$ | $1.20$ |
Higher modes are heavily damped, for $k\ge10$ the damping being even overcritical. The participation of these modes, however, should not play an important role.
The computation is executed with the following commands:
- beam53d3.bat
rmd3 beam53d3.i1 rpd3 beam53d3.i2 srh3 beam53d3.i3 hmot beam53d3.iM hcre beam53d3.iC hfro beam53d3.iR hnew beam53d3.iW
Input
- beam53d3.i1
; NELEM NNOD ITED IP 4 5 53 ; CRIT SCALE ... RP 1.01 1 8*0 ; default values of cross-sectional characteristics ; A Ik Wk Ieta 2e-4 6.6666666666e-9 6.666666666666e-7 1.66666666666e-9 ; Weta Izeta Wzeta Px Py Pz 3.33333333333e-7 6.66666666666666e-9 6.666666666666e-7 0 1 0 XY N 1:5 X 5*0:1 Y 5*0 Z 5*0 EL E 1:4 N 1 2 2 3 3 4 4 5 EN EN
- beam53d3.i2
; KREST IP 1 ; E α ν ρ MP 1 T 1 V 2e11 0 0.3 7800 AS 1 /M 1 /B 0 N 1 EN EN
- beam53d3.i3
; KREST IP 1 EN EN
- beam53d3.iM
; KDIAG KPRIN IP 1 0 EN EN
- beam53d3.iC
; NVEC IP 0 ; ALPHA BETA RP 5.3495239E-4 8.8663179 EN EN
- beam53d3.iR
; 0 KDAMP IP 0 1 ; PIVOT SHIFT TSTEP RP 100 0 7.640428e-3 EN EN
- beam53d3.iW
; KOUT KDUMP KPRIN KKIN KREST KGRAF IP 1 0 0 1 1 0 ; TEND RP 0.61123424 VC 1 T 1 ; directional vector R 0 0 1 0 0 0 4*(6*0) ; amplitude R 0.001 ; ang. frequency R 25.698761 ; output times R 17*0.48898739:0.61123424 ; use the first term of Fourier's series RS 2 T 1 I 1 0 ; direction, amplitude, frequency, times AS 3 T 1 I 1 3 I 2 5 I 3 6 I 4 9 EN EN
Output
- beam53d3.oW
; KOUT KDUMP KPRIN KKIN KREST KGRAF IP 1 0 0 1 1 0 ; TEND RP 0.61123424 VC 1 T 1 ; directional vector R 0 0 1 0 0 0 4*(6*0) ; amplitude R 0.001 ; ang. frequency R 25.698761 ; output times R 17*0.48898739:0.61123424 ; use the first term of Fourier's series RS 2 T 1 I 1 0 ; direction, amplitude, frequency, times AS 3 T 1 I 1 3 I 2 5 I 3 6 I 4 9 EN EN RIGHT-HAND SIDE ASSIGNED DAMPING INCLUDED ----------------------------- INFORMATION ----------------------------- CHOSEN TIME STEP TSTEP : 0.7640E-02 [s] FINISHING TIME TEND : 0.6112E+00 [s] ------------------------------------------------------------------------ TIME T = 0.488987E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 -0.49534E-009 2 0.00000E+000 0.00000E+000 -0.19499E-004 3 0.00000E+000 0.00000E+000 -0.65921E-004 4 0.00000E+000 0.00000E+000 -0.12509E-003 5 0.00000E+000 0.00000E+000 -0.18791E-003 TIME T = 0.496628E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.19509E-003 2 0.00000E+000 0.00000E+000 0.18284E-003 3 0.00000E+000 0.00000E+000 0.15315E-003 4 0.00000E+000 0.00000E+000 0.11511E-003 5 0.00000E+000 0.00000E+000 0.74565E-004 TIME T = 0.504268E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.38268E-003 2 0.00000E+000 0.00000E+000 0.37811E-003 3 0.00000E+000 0.00000E+000 0.36648E-003 4 0.00000E+000 0.00000E+000 0.35079E-003 5 0.00000E+000 0.00000E+000 0.33377E-003 TIME T = 0.511909E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.55557E-003 2 0.00000E+000 0.00000E+000 0.55916E-003 3 0.00000E+000 0.00000E+000 0.56660E-003 4 0.00000E+000 0.00000E+000 0.57516E-003 5 0.00000E+000 0.00000E+000 0.58382E-003 TIME T = 0.519549E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.70711E-003 2 0.00000E+000 0.00000E+000 0.71924E-003 3 0.00000E+000 0.00000E+000 0.74716E-003 4 0.00000E+000 0.00000E+000 0.78159E-003 5 0.00000E+000 0.00000E+000 0.81770E-003 TIME T = 0.527190E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.83147E-003 2 0.00000E+000 0.00000E+000 0.85262E-003 3 0.00000E+000 0.00000E+000 0.90178E-003 4 0.00000E+000 0.00000E+000 0.96324E-003 5 0.00000E+000 0.00000E+000 0.10280E-002 TIME T = 0.534830E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.92388E-003 2 0.00000E+000 0.00000E+000 0.95397E-003 3 0.00000E+000 0.00000E+000 0.10247E-002 4 0.00000E+000 0.00000E+000 0.11135E-002 5 0.00000E+000 0.00000E+000 0.12073E-002 TIME T = 0.542470E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.98079E-003 2 0.00000E+000 0.00000E+000 0.10194E-002 3 0.00000E+000 0.00000E+000 0.11106E-002 4 0.00000E+000 0.00000E+000 0.12260E-002 5 0.00000E+000 0.00000E+000 0.13482E-002 TIME T = 0.550111E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.10000E-002 2 0.00000E+000 0.00000E+000 0.10462E-002 3 0.00000E+000 0.00000E+000 0.11561E-002 4 0.00000E+000 0.00000E+000 0.12954E-002 5 0.00000E+000 0.00000E+000 0.14430E-002 TIME T = 0.557751E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.98079E-003 2 0.00000E+000 0.00000E+000 0.10333E-002 3 0.00000E+000 0.00000E+000 0.11582E-002 4 0.00000E+000 0.00000E+000 0.13171E-002 5 0.00000E+000 0.00000E+000 0.14857E-002 TIME T = 0.565392E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.92388E-003 2 0.00000E+000 0.00000E+000 0.98058E-003 3 0.00000E+000 0.00000E+000 0.11161E-002 4 0.00000E+000 0.00000E+000 0.12887E-002 5 0.00000E+000 0.00000E+000 0.14720E-002 TIME T = 0.573032E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.83147E-003 2 0.00000E+000 0.00000E+000 0.89002E-003 3 0.00000E+000 0.00000E+000 0.10302E-002 4 0.00000E+000 0.00000E+000 0.12092E-002 5 0.00000E+000 0.00000E+000 0.13996E-002 TIME T = 0.580673E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.70711E-003 2 0.00000E+000 0.00000E+000 0.76481E-003 3 0.00000E+000 0.00000E+000 0.90337E-003 4 0.00000E+000 0.00000E+000 0.10805E-002 5 0.00000E+000 0.00000E+000 0.12689E-002 TIME T = 0.588313E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.55557E-003 2 0.00000E+000 0.00000E+000 0.60971E-003 3 0.00000E+000 0.00000E+000 0.73979E-003 4 0.00000E+000 0.00000E+000 0.90640E-003 5 0.00000E+000 0.00000E+000 0.10837E-002 TIME T = 0.595953E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.38268E-003 2 0.00000E+000 0.00000E+000 0.43047E-003 3 0.00000E+000 0.00000E+000 0.54568E-003 4 0.00000E+000 0.00000E+000 0.69338E-003 5 0.00000E+000 0.00000E+000 0.85072E-003 TIME T = 0.603594E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.19509E-003 2 0.00000E+000 0.00000E+000 0.23421E-003 3 0.00000E+000 0.00000E+000 0.32858E-003 4 0.00000E+000 0.00000E+000 0.44986E-003 5 0.00000E+000 0.00000E+000 0.57914E-003 TIME T = 0.611234E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.61917E-009 2 0.00000E+000 0.00000E+000 0.28453E-004 3 0.00000E+000 0.00000E+000 0.97400E-004 4 0.00000E+000 0.00000E+000 0.18608E-003 5 0.00000E+000 0.00000E+000 0.28068E-003 * END OF HNEW * TOTAL CPU: 00:00:00