en:example:dyn:3:1
Table of Contents
Mode superposition, BEAM53D2
Problem
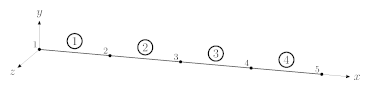
Mesh
| element | type | nodes |
|---|---|---|
| 1 | 53 | 1 2 |
| 2 | 53 | 2 3 |
| 3 | 53 | 3 4 |
| 4 | 53 | 4 5 |
Boundary conditions
$u=v=w=\varphi_x=\varphi_y=\varphi_z=0$ at node 1
Solution
In the mode superposition method we directly combine the eigenvectors neglecting the phase shift due to damping.
- beam53d2.bat
rmd3 beam53d2.i1 rpd3 beam53d2.i2 srh3 beam53d2.i3 fefs beam53d2.i4 hmot beam53d2.iM heig beam53d2.iE hmod beam53d2.iD
Input
- beam53d2.i1
; NELEM NNOD ITED IP 4 5 53 ; CRIT SCALE ... RP 1.01 1 8*0 ; default values of cross-sectional characteristics ; A Ik Wk Ieta 2e-4 6.6666666666e-9 6.666666666666e-7 1.66666666666e-9 ; Weta Izeta Wzeta Px Py Pz 3.33333333333e-7 6.66666666666666e-9 6.666666666666e-7 0 1 0 XY N 1:5 X 5*0:1 Y 5*0 Z 5*0 EL E 1:4 N 1 2 2 3 3 4 4 5 EN EN
- beam53d2.i2
; KREST IP 1 ; E α ν ρ MP 1 T 1 V 2e11 0 0.3 7800 AS 1 /M 1 /B 0 N 1 EN EN
- beam53d2.i3
; KREST IP 1 EN EN
- beam53d2.i4
; KREST IP 1 EN EN
- beam53d2.iM
; KDIAG KPRIN IP 1 0 EN EN
- beam53d2.iE
; KREST NROOT NITERX KTPR KEVP IP 1 10 0 0 0 EN EN
- beam53d2.iD
; KOUT KDUMP KPRIN KKIN IP 3 0 0 1 ; TEND DT RP 0 0 VC 1 T 1 ; directional vector R 0 0 1 0 0 0 4*(6*0) ; amplitude R 0.001 ; ang. frequency R 25.698761 ; damping R 10*0.1 ; use the first term of Fourier's series RS 2 T 1 I 1 0 ; direction, amplitude, frequency, damping AS 3 T 1 I 1 3 I 2 5 I 3 6 I 4 8 EN EN
Output
- beam53d2.oD
; KOUT KDUMP KPRIN KKIN IP 3 0 0 1 ; TEND DT RP 0 0 VC 1 T 1 ; directional vector R 0 0 1 0 0 0 4*(6*0) ; amplitude R 0.001 ; ang. frequency R 25.698761 ; damping R 10*0.1 ; use the first term of Fourier's series RS 2 T 1 I 1 0 ; direction, amplitude, frequency, damping AS 3 T 1 I 1 3 I 2 5 I 3 6 I 4 8 EN EN RIGHT-HAND SIDE ASSIGNED DAMPING INCLUDED SUM OF REACTIONS -0.1353409505777549E-07 0.7209223447460681E-09 -0.1101235522045654E+01 REACTIONS 1 -0.13534E-007 0.72092E-009 -0.11012E+001 2 0.00000E+000 0.00000E+000 0.00000E+000 3 0.00000E+000 0.00000E+000 0.00000E+000 4 0.00000E+000 0.00000E+000 0.00000E+000 5 0.00000E+000 0.00000E+000 0.00000E+000 AMPLITUDE OF THE STATIONARY SOLUTION TIME T = 0.000000E+00 [s] U [m] V [m] W [m] ALPHA [rad] BETA [rad] DISPLACEMENT 1 0.00000E+000 0.00000E+000 0.10000E-002 2 0.84588E-016 0.11155E-015 0.10530E-002 3 0.64241E-016 -0.26857E-016 0.11796E-002 4 -0.35034E-016 -0.18142E-015 0.13409E-002 5 -0.90682E-016 -0.34390E-015 0.15122E-002 VELOCITY 1 0.00000E+000 0.00000E+000 0.25699E-001 2 0.21738E-014 0.28667E-014 0.27061E-001 3 0.16509E-014 -0.69020E-015 0.30314E-001 4 -0.90034E-015 -0.46623E-014 0.34460E-001 5 -0.23304E-014 -0.88379E-014 0.38863E-001 ACCELERATION 1 0.00000E+000 0.00000E+000 0.66043E+000 2 0.55864E-013 0.73671E-013 0.69544E+000 3 0.42426E-013 -0.17737E-013 0.77904E+000 4 -0.23138E-013 -0.11982E-012 0.88557E+000 5 -0.59889E-013 -0.22712E-012 0.99873E+000 * END OF HMOD * TOTAL CPU: 00:00:00
en/example/dyn/3/1.txt · Last modified: 2022-03-15 08:29 by Petr Pařík