Obsah
Standardní model
V této příloze je popsán „standardní“ model nelineárního materiálu implementovaný v systému PMD.
Invarianty tenzoru napětí
Definujeme standardní invarianty $I_1,$ $J_2$ a $J_3$ tenzoru napětí $\sigma_{ij}$ \begin{align} I_1 &= \sigma_{kk}=\sigma_{11}+\sigma_{22}+\sigma_{33},\\ J_2 &= \frac{1}{2}s_{ij}s_{ij},\\ J_3 &= \frac{1}{3}s_{ij}s_{jk}s_{ki}=\det\left|\begin{array}{lll} s_{11} & s_{12} & s_{13} \\ s_{21} & s_{22} & s_{23} \\ s_{31} & s_{32} & s_{33} \end{array}\right|, \end{align} kde $s_{ij}$ je deviátor tenzoru napětí $$s_{ij} = \sigma_{ij}-\frac{1}{3}\delta_{ij}I_1$$ a $\delta_{ij}$ je Kroneckerovo delta.
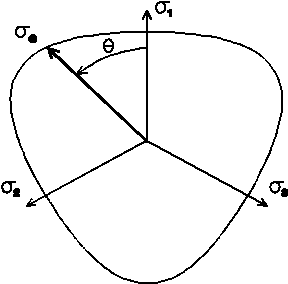
V systému PMD se používá jiná, ekvivalentní trojice invariantů, a to střední napětí $$\sigma_m = \frac{1}{3}I_1,$$ von Misesovo efektivní napětí $$\sigma_e = \sqrt{3J_2}$$ a Lodeho podobnostní parametr $$\mu = \cos(3\theta)=\frac{27}{2}\frac{J_3}{\sigma_e^3}.$$ Úhel $\theta$ směřuje od osy hlavního napětí $\sigma_1$ k bodu znázorňujícímu napjatost v deviátorové rovině, viz Obr. 1.
Vyjádříme dále derivace $\sigma_m,$ $\sigma_e$ a $\mu$ podle $\sigma_{ij}$: \begin{align} \frac{\partial\sigma_m}{\partial\sigma_{ij}} &= \frac{1}{3}\delta_{ij},\\ \frac{\partial\sigma_e}{\partial\sigma_{ij}} &= \frac{3}{2}\frac{s_{ij}}{\sigma_e},\tag{1}\label{1-8}\\ \frac{\partial\mu}{\partial\sigma_{ij}} &= \frac{27}{2}\frac{s_{ik}s_{kj}}{\sigma_e^3}-\frac{9}{2}\frac{\mu}{\sigma_e^2}s_{ij}-3\frac{\delta_{ij}}{\sigma_e}. \end{align}
Uvažujme speciální případ jednoosé napjatosti, kdy $\sigma_{11}=\sigma$ a ostatní složky tenzoru napětí jsou nulové. Potom \begin{align} \sigma_m &= \frac{1}{3}\sigma,\\ \sigma_e &= |\sigma|,\\ \mu &= \pm1. \end{align} Znaménka $\pm$ u invariantu $\mu$ rozlišují případy jednoosého tahu ($+$) a jednoosého tlaku ($-$).
Pro derivace v případě jednoosé napjatosti platí \begin{align} \frac{\partial\sigma_m}{\partial\sigma_{ij}} &= 0 \quad i\ne j,\quad \frac{\partial\sigma_m}{\partial\sigma_{11}} = \frac{\partial\sigma_m}{\partial\sigma_{22}} = \frac{\partial\sigma_m}{\partial\sigma_{33}} = \frac{1}{3},\\ \frac{\partial\sigma_e}{\partial\sigma_{ij}} &= 0 \quad i\ne j,\quad \frac{\partial\sigma_e}{\partial\sigma_{11}} = \pm1, \quad \frac{\partial\sigma_e}{\partial\sigma_{22}} = \frac{\partial\sigma_e}{\partial\sigma_{33}} = \mp\frac{1}{2},\tag{2}\label{1-10}\\ \frac{\partial\mu}{\partial\sigma_{ij}} &= 0. \end{align}
Zobecněná podmínka plasticity
Podmínku plasticity lze vyjádřit v závislosti na invariantech $\sigma_m,$ $\sigma_e,$ $\mu$ a teplotě $T$ jako $$F(\sigma_{ij},T) = \sigma_e-Y(\sigma_m,\mu,T) = 0.\tag{3}\label{2-1}$$
Vztah \eqref{2-1} definuje funkci $$\sigma_e = Y(\sigma_m,\mu,T),$$ která popisuje tvar plochy plasticity v prostoru napětí.
Obr. 1: Závislost $Y$ na $\mu=\cos(3\theta)$ představuje řez plochy plasticity deviátorovou rovinou.
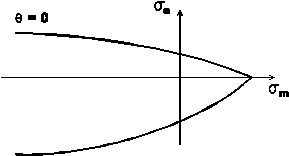
Obr. 2: Závislost $Y$ na $\sigma_m$ vyjadřuje citlivost vůči hydrostatické napjatosti a odpovídá meridiánovému řezu plochy plasticity.
Gradient mezní funkce $F$ v prostoru napětí má tvar $$\frac{\partial F}{\partial\sigma_{ij}} = \frac{\partial\sigma_e}{\partial\sigma_{ij}}-\frac{\partial Y}{\partial\sigma_m}\frac{\partial\sigma_m}{\partial\sigma_{ij}}-\frac{\partial Y}{\partial\mu}\frac{\partial\mu}{\partial\sigma_{ij}}.\tag{4}\label{2-3}$$
Ve speciálním případě jednoosé napjatosti, kdy $\sigma_{11}=\sigma$ a ostatní složky tenzoru napětí jsou nulové, dostáváme s ohledem na \eqref{1-10} \begin{align} \frac{\partial F}{\partial\sigma_{ij}} &= 0 \quad i\ne j,\\ \frac{\partial F}{\partial\sigma_{11}} &= \pm1-\frac{1}{3}\frac{\partial Y}{\partial\sigma_m},\tag{5}\label{2-4}\\ \frac{\partial F}{\partial\sigma_{22}} &= \frac{\partial F}{\partial\sigma_{33}} = \mp\frac{1}{2}-\frac{1}{3}\frac{\partial Y}{\partial\sigma_m}. \end{align}
Horní znaménka příslušejí případu jednoosého tahu $\sigma>0$ a dolní znaménka odpovídají jednoosému tlaku $\sigma<0.$
Asociovaný a neasociovaný zákon tečení
Směr plastického toku se specifikuje směrovým tensorem $R_{ij}$ $$\dot\varepsilon_{ij}^p = \lambda R_{ij},\quad \lambda>0.\tag{6}\label{3-1}$$
Nejčastěji se používá asociovaný zákon tečení, kdy $$R_{ij} = \frac{\partial F}{\partial\sigma_{ij}}.\tag{7}\label{3-2}$$
Tomu podle \eqref{2-3} a úžením \eqref{1-8} odpovídá poměrná změna objemu $$\dot\varepsilon_{kk}^p = \lambda\frac{\partial F}{\partial\sigma_{kk}} = -\lambda\frac{\partial Y}{\partial\sigma_m}.$$
U podmínek plasticity závisejících na tlaku je $Y$ klesající vzhledem k $\sigma_m,$ viz Obr. 2. Derivace $\partial Y/\partial\sigma_m$ je tudíž záporná a asociovaný zákon tečení implikuje kladnou objemovou změnu. Tato predikce však neodpovídá skutečnosti, a proto se někdy používá neasociovaný zákon tečení, nejčastěji ve tvaru $$R_{ij} = \frac{3}{2}\frac{s_{ij}}{\sigma_e}+\Phi\delta_{ij}.\tag{8}\label{3-4}$$
Poměrná změna objemu je potom $$\dot\varepsilon_{kk}^p = 3\lambda\Phi$$ a veličinu $\Phi,$ která se nazývá dilatačním faktorem, je možné nastavit experimentálně. Pokud $\Phi=0,$ \eqref{3-4} představuje Prandtl-Reussovy rovnice s nulovou objemovou změnou.
Efektivní deformace
Rychlost efektivní deformace definujeme jako $$\dot\varepsilon_p = \sqrt{\gamma\dot\varepsilon_{ij}^p\dot\varepsilon_{ij}^p},$$ kde $\gamma$ je definitorický parametr. Podle \eqref{3-1} je $$\dot\varepsilon_p = \lambda\sqrt{\gamma R_{ij}R_{ij}}$$ a rovnice tečení má tvar $$\dot\varepsilon_p = \frac{\dot\varepsilon_p}{\sqrt\gamma}\rho_{ij},\quad \rho_{ij} = \frac{R_{ij}}{\sqrt{R_{kl}R_{kl}}}.\tag{9}\label{4-3}$$
Parametr $\gamma$ volíme tak, aby při jednoosé napjatosti $\sigma_{11}=\sigma$ platilo $\dot\varepsilon_p=|\dot\varepsilon_{11}^p|,$ neboli $$\gamma = \rho_{11}^2.\tag{10}\label{4-4}$$
Pro asociovaný zákon tečení tak podle \eqref{2-4} dostáváme $$\gamma = \frac{\left(\pm1-\frac{1}{3}\frac{\partial Y}{\partial\sigma_m}\right)^2}{\frac{3}{2}+\frac{1}{3}\left(\frac{\partial Y}{\partial\sigma_m}\right)^2}\tag{11}\label{4-5}$$ a pro neasociovaný zákon \eqref{3-4} $$\gamma = \frac{(\pm1+\Phi)^2}{\frac{3}{2}+3\Phi^2}.\tag{12}\label{4-6}$$
Horní znaménko přitom platí pro tahovou kalibraci modelu (tj. platí pro případ $\sigma_{11}>0$), zatímco dolní znaménko odpovídá tlakové kalibraci (kdy $\sigma_{11}<0$). V systému PMD byla zvolena tlaková kalibrace a ve vzorcích \eqref{4-5}, \eqref{4-6} platí dolní znaménka. Ve speciálním případě $\partial Y/\partial\sigma_m=0$ nebo $\Phi=0$ je vždy $\gamma=2/3.$
U neasociovaného zákona platí bez ohledu na stav napjatosti $$R_{kl}R_{kl} = \frac{3}{2}+3\Phi^2,$$ takže dosazením za $\gamma$ (při tlakové kalibraci) a $R_{kl}R_{kl}$ do \eqref{4-3} $$\dot\varepsilon_{ij}^p = \frac{\dot\varepsilon_p}{|1-\Phi|}R_{ij},$$ kde $R_{ij}$ je dáno výrazem \eqref{3-4}. Úžením tenzoru $R_{ij}$ dostáváme poměrnou objemovou změnu $$\dot\varepsilon_{kk}^p = \frac{3\Phi}{|1-\Phi|}\dot\varepsilon_p\tag{13}\label{4-9}$$ a dilatační faktor $\Phi$ může být experimentálně určen.
Kombinované zpevnění
Pro zpevňující materiály se podmínka plasticity \eqref{2-1} upraví následujícím způsobem: namísto tenzoru napětí $\sigma_{ij}$ se dosadí napěťová veličina $\tau_{ij}=\sigma_{ij}-h_{ij},$ kde $h_{ij}$ je tenzor kinematických parametrů (backstress), a závislost funkce $Y$ se rozšíří o efektivní deformaci $\varepsilon_p$ $$F(\sigma_{ij}-h_{ij},\varepsilon_p,T) = \sigma_e-Y(\sigma_m,\mu,\varepsilon_p,T) = 0,\tag{14}\label{5-1}$$ přičemž invarianty $\sigma_e,$ $\sigma_m$ a $\mu$ jsou vyjádřeny pro $\tau_{ij}.$ Platí $$\frac{\partial F}{\partial\sigma_{ij}} = \frac{\partial F}{\partial\tau_{ij}} = -\frac{\partial F}{\partial h_{ij}}.\tag{15}\label{5-2}$$
Jako evoluční rovnice pro $h_{ij}$ je použit Pragerův model $$h_{ij} = \kappa\frac{\partial F}{\partial\sigma_{ij}}.\tag{16}\label{5-3}$$
Funkci $Y$ je možné rozložit na izotropní a kinematickou složku $$Y(\sigma_m,\mu,\varepsilon_p,T) = \sigma_Y(\sigma_m,\mu,\varepsilon_p,T)-Q_Y(\varepsilon_p),\tag{17}\label{5-4}$$ takže volbou $Q_Y(\varepsilon_p)$ obdržíme různé modely zpevnění. Označme $T_o$ výchozí teplotu odpovídající stavu $\sigma_{ij}\equiv0$ a máme:
- Izotropní zpevnění $$Q_Y^\text{iso}(\varepsilon_p)\equiv0$$
- Kinematické zpevnění $$Q_Y^\text{kin}(\varepsilon_p)\equiv\sigma_Y(0,0,\varepsilon_p,T_o)-\sigma_Y(0,0,0,T_o)$$
- Kinematicko-izotropní cyklické zpevnění $$Q_Y^\text{hrd}(\varepsilon_p)<Q_Y^\text{kin}(\varepsilon_p)$$
- Kinematicko-izotropní cyklické změkčení $$Q_Y^\text{sft}(\varepsilon_p)>Q_Y^\text{kin}(\varepsilon_p)$$
V průběhu plastického toku musí být splněna podmínka konzistence $$\dot F = \frac{\partial F}{\partial\sigma_{ij}}\dot\sigma_{ij}+\frac{\partial F}{\partial h_{kl}}\dot h_{kl}+\frac{\partial F}{\partial\varepsilon_p}\dot\varepsilon_p+\frac{\partial F}{\partial T}\dot T = 0.\tag{18}\label{5-5}$$
Využijeme rozklad \eqref{5-4} a označíme $$H' = \frac{\partial\sigma_Y}{\partial\varepsilon_p},\quad Q' = \frac{dQ_Y}{d\varepsilon_p}.$$
Dosazením do \eqref{5-5} a pomocí \eqref{5-2} dostáváme $$\frac{\partial F}{\partial\sigma_{ij}}\dot\sigma_{ij}-\frac{\partial F}{\partial\sigma_{kl}}\dot h_{kl}-H'\dot\varepsilon_p+Q'\dot\varepsilon_p-\frac{\partial\sigma_Y}{\partial T}\dot T = 0.\tag{19}\label{5-7}$$
Dále předpokládáme, že přírůstek kinematických parametrů závisí výhradně na $Q',$ odkud $$\frac{\partial F}{\partial\sigma_{kl}}\dot h_{kl} = Q'\dot\varepsilon_p$$ a multiplikátor $\kappa$ v Pragerově modelu \eqref{5-3} lze vyčíslit jako $$\kappa = \frac{Q'\dot\varepsilon_p}{g^2},\quad g^2 = \frac{\partial F}{\partial\sigma_{kl}}\frac{\partial F}{\partial\sigma_{kl}}.\tag{20}\label{5-9}$$
Rovnice konzistence \eqref{5-7} se zjednoduší na $$\frac{\partial F}{\partial\sigma_{ij}}\dot\sigma_{ij}-\frac{\partial\sigma_Y}{\partial T}\dot T = H'\dot\varepsilon_p.\tag{21}\label{5-10}$$
Zobecněný model plasticity
Podmínka plasticity má tvar \eqref{5-1} $$F(\sigma_{ij}-h_{ij},\varepsilon_p,T) = \sigma_e-Y(\sigma_m,\mu,\varepsilon_p,T) = 0.$$
Funkci $Y$ rozložíme jako v \eqref{5-4} $$Y(\sigma_m,\mu,\varepsilon_p,T) = \sigma_Y(\sigma_m,\mu,\varepsilon_p,T)-Q_Y(\varepsilon_p).$$
Pragerovo kinematické zpevnění \eqref{5-3} a \eqref{5-9} dává $$\dot h_{ij} = Q'\frac{\dot\varepsilon_p}{g^2}\frac{\partial F}{\partial\sigma_{ij}}.$$
Zákon tečení zapíšeme v obecném tvaru \eqref{4-3} $$\dot\varepsilon_{ij}^p = \frac{\dot\varepsilon_p}{\sqrt\gamma}\rho_{ij},$$ kde jednotkový směrový tenzor $\rho_{ij}$ vyplývá z \eqref{3-2} nebo \eqref{3-4}.
Zbývá určit $\dot\varepsilon_p,$ neboť potom z Hookeova zákona $$\dot\sigma_{ij} = D_{ijkl}(\dot\varepsilon_{kl}-\dot\varepsilon_{kl}^o-\dot\varepsilon_{kl}^p)\tag{22}\label{6-5}$$ plyne rychlost napětí. Deformace $\dot\varepsilon_{kl}^o$ se skládá z creepové složky a teplotní dilatace s koeficientem roztažnosti $\alpha$ $$\dot\varepsilon_{kl}^o = \dot\varepsilon_{kl}^c+\alpha\dot T\delta_{kl}$$ a je předem známa. Dosazením \eqref{6-5} do rovnice konzistence \eqref{5-10} a rozřešením vzhledem k $\dot\varepsilon_p$ dostáváme $$\dot\varepsilon_p = \frac{\frac{\partial F}{\partial\sigma_{ij}}D_{ijkl}(\dot\varepsilon_{kl}-\dot\varepsilon_{kl}^o)-\frac{\partial\sigma_Y}{\partial T}\dot T}{H'+\frac{\partial F}{\partial\sigma_{mn}}D_{mnpq}\frac{\rho_{pq}}{\sqrt\gamma}}.$$
Izotropní model creepu
Pro izotropní creep volíme jednotkový směrový tensor $\rho_{ij}$ pevně $$\dot\varepsilon_{ij}^c = \lambda\rho_{ij},\quad \rho_{ij} = \sqrt{\frac{3}{2}}\frac{s_{ij}}{\sigma_e}.\tag{23}\label{7-1}$$
Při jednoosé napjatosti $\sigma_{11}=\sigma$ je $\rho_{11}^2=2/3$ a podle \eqref{4-4} platí pro parametr $\gamma=2/3=\text{konst.}$ Efektivní creepová deformace je tudíž definována jako $$\dot\varepsilon_c = \sqrt{\frac{2}{3}\dot\varepsilon_{ij}^c\dot\varepsilon_{ij}^c}$$ a při jednoosé napjatosti je $\dot\varepsilon_c=|\dot\varepsilon_{11}^c|.$ Dosazením do \eqref{7-1} máme $$\dot\varepsilon_{ij}^c = \frac{3}{2}\frac{\dot\varepsilon_c}{\sigma_e}s_{ij}.$$
Rychlost creepové deformace $\dot\varepsilon_{ij}^c$ je nyní explicitně určena stavem materiálu, protože závislost $$\dot\varepsilon_c = \dot\varepsilon_c(\sigma_e,\varepsilon_c,T)\tag{24}\label{7-4}$$ se odečte z jednoosých creepových křivek. Ze struktury funkce \eqref{7-4} vyplývá, že přechod z jedné křivky na druhou probíhá při konstantní efektivní deformaci $\varepsilon_c$ neboli podle hypotézy deformačního zpevnění (strain hardening).
V systému PMD se elastoplastický model a creepový model kombinují podle následujících pravidel:
- Inelastické složky deformace se sčítají, tj. $$\varepsilon_{ij} = \varepsilon_{ij}^e+\alpha T\delta_{ij}+\varepsilon_{ij}^I,\quad \varepsilon_{ij}^I = \varepsilon_{ij}^p+\varepsilon_{ij}^c,$$ kde $\varepsilon_{ij}^e$ je elastická deformace, kterou lze kdykoliv vypočítat z napětí pomocí Hookeova zákona, a $\varepsilon_{ij}^I$ je trvalá deformace.
- Efektivní deformace $\varepsilon_p$ a $\varepsilon_c$ jsou na sobě nezávislé.
Vstupní veličiny
Materiálové veličiny se definují v souboru name.i2, přičemž veličiny $\sigma_Y,Q_Y,{\dot\varepsilon}_c,\Phi$ se zapíší na 5.–8. pozici sady:
MP číslo sady T 1 V $E$ $\alpha$ $\nu$ $\rho$ $\sigma_Y$ $Q_Y$ ${\dot\varepsilon}_c$ $\Phi$
Při definici materiálových veličin lze využít všech funkčních závislostí.
V případě, že některé pozice uvnitř MP sady nejsou použity (viz dále), musí být formálně zapsány jako 0.
Typ modelu plasticity se rozlišuje klíčem $\mathtt{KMOD}$ v souboru name.iP.
Výpočet creepu se aktivuje klíčem $\mathtt{KCRP}=1$ v souboru name.iP bez ohledu na hodnotu $\mathtt{KMOD}.$ Pro $\mathtt{KCRP}=1$ je vždy nutné zadat závislost $\dot\varepsilon_c=\dot\varepsilon_c(\sigma_e,\varepsilon_c,T).$ Pokud rychlost creepové deformace nezávisí na $\varepsilon_c,$ probíhá tečení v oblasti sekundárního creepu.
Elasticita ($\mathtt{KMOD}=0$)
Plastické konstitutivní vztahy jsou vypnuty, čehož se dá využít např. pro výpočet samostatné creepové úlohy.
Von Misesův model – J₂ teorie ($\mathtt{KMOD}=1$)
Zadává se funkce $\sigma_Y(\varepsilon_p,T),$ kterou je možné kalibrovat na jednoosé tahové zkoušce, kdy $\sigma_{11}=\sigma_Y(\varepsilon_{11}^p,T).$ Pokud je $\sigma_Y$ pouze funkcí teploty $T$ nebo je konstantní, je materiál považován za ideálně plastický. Dále se zadává kinematická složka zpevnění $Q_Y(\varepsilon_p).$
Zobecněný asociovaný model ($\mathtt{KMOD}=2$)
Zadává se totéž, co v případě $\mathtt{KMOD}=1,$ avšak funkce $\sigma_Y$ je rozšířena o dva invarianty napětí $\sigma_m$ a $\mu.$ Závislost $\sigma_Y(\sigma_m,\mu,\varepsilon_p,T)$ tak umožňuje zadat libovolnou podmínku plasticity. Funkce $\sigma_Y$ se kalibruje na případě jednoosého tlaku, pro který platí $\sigma_{11}=\sigma_Y(\sigma_{11}/3,-1,\varepsilon_{11}^p,T).$
Zobecněný neasociovaný model ($\mathtt{KMOD}=3$)
Zadává se totéž, co v případě $\mathtt{KMOD}=2.$ Navíc je nutné zadat dilatační faktor (objemovou roztažnost plastických deformací) $\Phi,$ který se kalibruje pomocí rovnice \eqref{4-9}.